1. Прямая, пересекающая плоскость, называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей и этой плоскости.

2. Дана плоскость , прямая a € , прямая b, пересекающая , и пусть с - проекция прямой b на плоскость . Eсли ba, то с a. Обратно, если с a, то b а (теорема о трех перпендикулярах) (рис. 20).

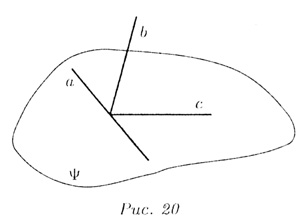
3. Даны две плоскости и , пересекающиеся по прямой a. Пусть b₁ - прямая. лежащая в , и

b₁ ;

b₂ - прямая, лежащая в , и b₂ . Тогда угол между и определяется как угол между b₁ и b₂.

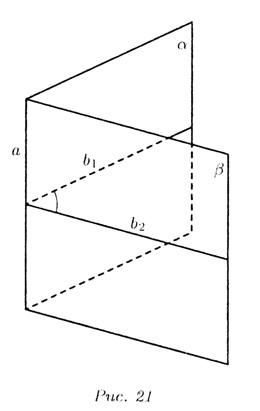
(рис. 21).

Если

4. Две прямые называются скрещивающимися, если они не пересекаются и но лежат в одной плоскости. Расстоянием между ними называется длина, их общего перпендикуляра, равного расстоянию между параллельными плоскостями, проходящими через эти прямые. Угол между скрещивающимися прямыми равен углу между пересекающимися параллельными им прямыми (рис. 22).

5. Элементы призмы (рис. 23): параллельные основания (многоугольники), параллельные боковые ребра, боковые грани — параллелограммы, высота — расстояние между основаниями. У прямой призмы боковые ребра перпендикулярны основаниям. Правильная призма — это прямая призма, основания которой — правильные многоугольники.

Объем призмы V = S_осн • Н

Площадь боковой поверхности S_бок = S_осн • H_бок.гр

Площадь полной поверхности S_n = S_бок + 2 • S_осн.

Четырехугольная призма называется параллелепипедом, а если у него квадратные грани, то это куб.

6. Элементы пирамиды (рис. 24): основание - многоугольник, боковые ребра - отрезки, соединяющие вершину пирамиды с вершинами основания, боковые грани — треугольники. У правильной пирамиды основание - правильный многоугольник, боковые грани — равнобедренные треугольники. Высота боковой грани называется апофермой.

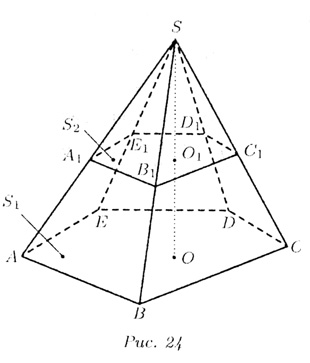
Треугольная пирамида называется тетраэдром.

Тетраэдр, все грани которого — правильные треугольники, называется правильным.

a) Если все боковые ребра пирамиды образуют с основанием ранные углы или если все боковые ребра равны, то высота пирамиды проходит через центр окружности, описанной около основания.

b) Коли все двугранные углы при основании равны а. то высота пирамиды приходит через центр окружности, вписанной в основание, и

c) Если пирамиду пересечь плоскостью, параллельной основанию, то:

• получится новый многогранник — усеченная пирамида;

• боковые ребра пирамиды и высота разделятся на пропорциональные части;

• в сечении получится многоугольник, подобный основанию;

• площадь сечения и площадь основания относятся как квадраты их расстоянии до вершины пирамиды.

Объем пирамиды

Объем усеченной пирамиды

7. Элементы прямого кругового цилиндра: основание — круг радиуса R, образующая — отрезок, соединяющий две точки окружностей оснований и перпендикулярный основаниям. Объем, площадь боковой и полной поверхностей цилиндра вычисляются по формулам:

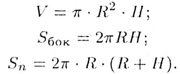
8. Элементы прямого кругового конуса: основание — круг радиуса R, образующая — отрезок, соединяющий вершину конуса с точкой окружности основания (L — длина образующей).

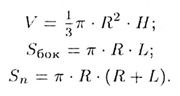
Объем усеченного конуса

Площадь боковой поверхности усеченного конуса (L — образующая усеченного конуса)

9. Объем тара радиуса R равен

Площадь поверхности шара