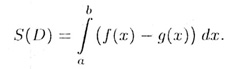1. Функция F(x) называется первообразной функции f(x) на отрезке [a,b], если
F'(x) = f(x).
Если
f(х) = cosx,
то
F(х) = sin x, х € R.
Если
f(х) = x3, то
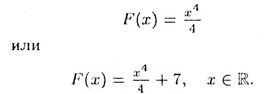
2. Множество всех первообразных
F(x) + С функции f(х), где С — произвольная постоянная, называется неопределенным интегралом от функции f(x) и обозначается
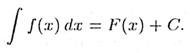
При этом f(x) называется подынтегральной функцией, f(x) dx — подынтегральным дифференциалом. Действие нахождения первообразной называется интегрированием.
3. Следующие свойства неопределенного интеграла вытекают из его определения.
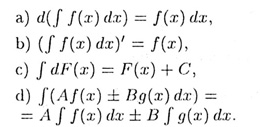
Свойство (d) выражает линейность действия интегрирования (A и В — постоянные).
4. Переменную интегрирования в таблице основных интегралов принимаем и, так как это удобно для применения.
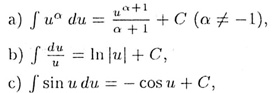
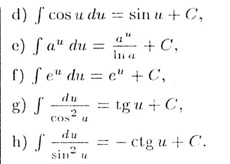
5. Если F(x) - произвольная ервообразная функции f(x) нa отрезке [a,b], то определенным интегралом

от функции f(x) вдоль отрезка [a,b] называется число
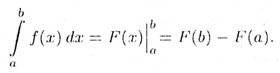
В правой части написано приращение первообразной f(x) на отрезке [а; b].
6. Если f(x) неотрицательна и непрерывна на отрезке [a;b], то фигура D, ограниченная снизу отрезком [а;b], сверху графиком Г функции f(x), а с боков отрезками прямых x = a, х = b, называется криволинейной трапецией.
Площадь S = S(D) фигуры D криволинейной трапеции вычисляется по формуле
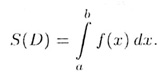
Если область D ограничена сверху графиком функции у = f(x), снизу графиком функции у = g(x), а с боков отрезками прямых х = а, х = b, то площадь S этой фигуры вычисляется по формуле