Даны две плоскости ![]() и
и ![]() ,
, ![]() ||
|| ![]() . В одной из них дана некоторая
фигура Ф. Пусть задана также некоторая прямая l, пересекающая данные плоскости.
Через каждую точку M фигуры Ф проведем отрезки MN, параллельные l и заключенные
между
. В одной из них дана некоторая
фигура Ф. Пусть задана также некоторая прямая l, пересекающая данные плоскости.
Через каждую точку M фигуры Ф проведем отрезки MN, параллельные l и заключенные
между ![]() и
и ![]() .
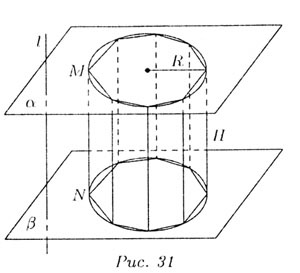
Множество всех этих отрезков MN образует некоторое тело, которое называется
цилиндром (рис. 31). Фигуры Ф и Ф1
(Ф1
— фигура, равная фигуре Ф) называются основаниями, а расстояние между
ними — высотой цилиндра. Если Ф - круг, а MN перпендикулярны плоскостям
.
Множество всех этих отрезков MN образует некоторое тело, которое называется
цилиндром (рис. 31). Фигуры Ф и Ф1
(Ф1
— фигура, равная фигуре Ф) называются основаниями, а расстояние между
ними — высотой цилиндра. Если Ф - круг, а MN перпендикулярны плоскостям
![]() и
и ![]() ,
то цилиндр называется прямым круговым или просто круглым.
,
то цилиндр называется прямым круговым или просто круглым.
Теорема. Объем круглого цилиндра радиуса R и высотой H вычисляется по формуле
![]()
Для получения объема прямого кругового цилиндра поступаем следующим образом. В основание цилиндра впишем правильный n-угольпик, где n — достаточно большое натуральное число. Проводя соответствующие отрезки МN через вершины вписанного многоугольника, получаем вписанную и цилиндр правильную призму, объем которой достаточно точно (при больших n) выражает объем цилиндра:
![]() - площадь многоугольника
(основания призмы), H — высота цилиндра, совпадает с высотой призмы. Если
R - радиус круга основания цилиндра, то
- площадь многоугольника
(основания призмы), H — высота цилиндра, совпадает с высотой призмы. Если
R - радиус круга основания цилиндра, то
![]()
Тем самым, приходим к формуле
![]()