Пусть ![]() — некоторая
плоскость, А -точка, не лежащая на
— некоторая
плоскость, А -точка, не лежащая на ![]() (рис. 34).
(рис. 34).
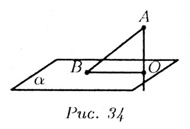
Проведем через А прямую, перпендикулярную к плоскости ![]() ,
и через О обозначим ее пересечение с
,
и через О обозначим ее пересечение с ![]() .
Отрезок АО называется перпендикуляром, проведенным из А к плоскости
.
Отрезок АО называется перпендикуляром, проведенным из А к плоскости ![]() ,
а О - основанием перпендикуляра.
,
а О - основанием перпендикуляра.
Если В — произвольная точка плоскости, отличная от О, то отрезок АВ
называется наклонной к плоскости, В — основание наклонной, а отрезок ОВ
— проекцией наклонной АВ на плоскости ![]() (рис. 34). Перпендикуляр АО отличается от всех наклонных АВ тем, что он
короче, т.е. АО < AB (АО — катет, АB — гипотенуза прямоугольного
(рис. 34). Перпендикуляр АО отличается от всех наклонных АВ тем, что он
короче, т.е. АО < AB (АО — катет, АB — гипотенуза прямоугольного ![]() АОВ). Другими словами, расстояние от точки А до точки О меньше, чем расстояние
от точки А до точки В. Это расстояние от А до О называется расстоянием
от точки .4 до плоскости
АОВ). Другими словами, расстояние от точки А до точки О меньше, чем расстояние
от точки А до точки В. Это расстояние от А до О называется расстоянием
от точки .4 до плоскости ![]() .
.
Когда мы говорим о расстоянии предмета, объекта до земли или высоте предмета над землей, то имеется в виду длина перпендикуляра от соответствующей точки к плоскости земли (например, высота самолета, облаков и т. п.).
Если прямая параллельна плоскости, то все ее точки находятся на одинаковом расстоянии от плоскости. Таким образом, расстоянием от прямой до параллельной плоскости называется расстояние от любой ее точки до этой плоскости.
Если две плоскости параллельны, то точки каждой из них равноудалены от другой плоскости. Таким образом, расстоянием между параллельными плоскостями называется расстояние от любой точки одной из этих плоскостей до другой плоскости.