Дан круговой конус радиуса R и образующий равной L: ОA = R, АВ = L (рис. 37,а).
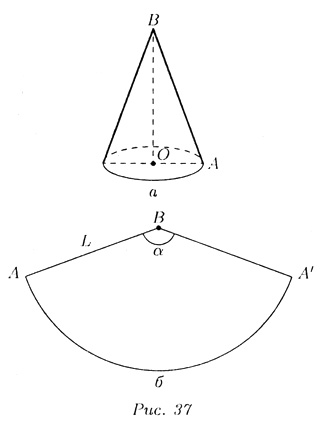
Разрежем конус по образующей AB и развернем его боковую поверхность (рис. 37,б). Получаем криволинейный треугольник АВА' с АВ = L и
![]()
Боковая поверхность Sб равна площади кругового сектора АВА'' радиуса L. Его площадь, как известно из планиметрии, равна
![]()
![]()
Чтобы найти угол ![]() воспользуемся
формулой длины дуги, стягивающей угол
воспользуемся
формулой длины дуги, стягивающей угол ![]() :
:
![]()
С другой стороны,
![]()
![]()
поскольку АА' есть на самом деле вытянутая по этой дуге окружность радиуса R основания конуса. Из равенства
![]()
находим
![]()
и эту величину подставим в формуле для S:
![]()
Таким образом, боковая поверхность конуса равна
![]()