Любые две пересекающиеся прямые расположены в одной плоскости
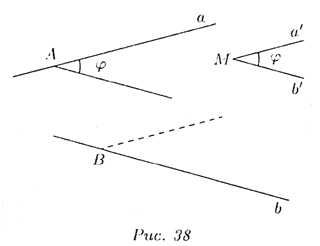
и образуют две пары смежных углов. Меньший из этих углов ![]() называется углом между пересекающимися прямыми (рис. 38).
называется углом между пересекающимися прямыми (рис. 38).
Пусть теперь а и b - две скрещивающиеся прямые. Возьмем произвольную
точку A на прямой ![]() и через нее
проведем прямую b1
параллельно прямой b. Угол
и через нее
проведем прямую b1
параллельно прямой b. Угол ![]() между прямыми а и b1
называется углом между скрещивающимися прямыми a н b (рис. 38).
между прямыми а и b1
называется углом между скрещивающимися прямыми a н b (рис. 38).
Это определение корректно потому, что полученный угол не зависит от положения взятой точки A на прямой. B самом деле, если на прямой a брать другую точку A1 и через нее пронести прямую b2|| b, то получим угол
![]()
как углы с взаимно параллельными сторонами.
Тот же угол ![]() получим в случае:
получим в случае:
1) если через произвольную точку В прямой b провести прямую a1|| a (рис. 38):
2) если через любую точку M пространства провести две прямые a'|| a и b'|| b. Угол между а' и b' можно также принять за угол между прямыми a и b (рис. 38).