Объем призмы ранен V = S_основ • H. где S_основ — площадь основания призмы. H — ее высота.

Исходим из известного факта: объем параллелепипеда, равен

V_пар = S_основ • H

(S_основ - площадь основания, H — высота).

Начнем с частного случая. Пусть нам дана треугольная призма.

Достроим ее до параллелепипеда. Следовательно, параллелепипед состоит из двух равных призм, поэтому

С другой стороны,

а высота призмы и параллелепипеда общая. Из равенства

следует, что

Переходим теперь к общему случаю. Дана произвольная призма. В ее основании лежит многоугольник. Проведя в нем диагонали, исходящие, из одной вершины, разбиваем многоугольник на треугольники (рис. 39). Сечения, проведенные через эти диагонали и соответствующие боковые ребра призмы делят ее на определенное число n треугольных призм. Для призмы с номером k объем равен

V_k = S_k • H

где S_k — площадь ее основания, H — высота первоначальной призмы. Складывая объем треугольных призм, получаем объем первоначальной призмы:

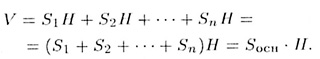
Формула установлена.