Дана плоскость ![]() и точка А вне этой плоскости.
и точка А вне этой плоскости.
Проекцией точки А на плоскость ![]() называется основание Q перпендикуляра, проведенного из этой точки к плоскости.
называется основание Q перпендикуляра, проведенного из этой точки к плоскости.
Пусть а — произвольная прямая, пересекающая плоскость ![]() в точке О, причем прямая а не перпендикулярна плоскости
в точке О, причем прямая а не перпендикулярна плоскости ![]() (рис. 40).
(рис. 40).
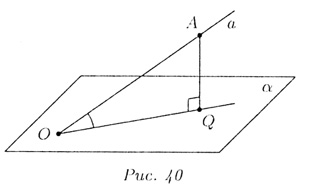
Прямая а и
перпендикуляр AQ (А €
а) определяют плоскость ![]() ,
, ![]() _|_
_|_ ![]() .
.
Прямая a1,
проходящая через точки О и Q, называется проекцией а на плоскость ![]() .
.
Углом между прямой а и плоскостью ![]() ,
пересекающей эту прямую и не перпендикулярной к ней, называется угол между
прямой а и ее проекцией a1
на плоскость
,
пересекающей эту прямую и не перпендикулярной к ней, называется угол между
прямой а и ее проекцией a1
на плоскость ![]() (рис. 40).
(рис. 40).
Если прямая а перпендикулярна плоскости ![]() ,
то ее проекцией на плоскость представляет собой точку О, а угол между
а и
,
то ее проекцией на плоскость представляет собой точку О, а угол между
а и ![]() считается прямым (равным
90°).
считается прямым (равным
90°).
Если прямая а параллельна плоскости ![]() ,
то угол между ними принимают равным нулю.
,
то угол между ними принимают равным нулю.