Объем пирамиды равен одной третьей произведения площади основания пирамиды на длину ее высоты:

Докажем эти формулу для треугольной пирамиды. Пусть дана пирамида (треугольная) DABC с основанием ABC площади S_основ и высотой DO = H (рис. 41). Исходим из объема призмы

V_пр = Sh.

Выполним следующие построения. Пусть n - некоторое натуральное число (на рисунке взято n = 5, а впоследствии будем считать n очень большим).

1. Высоту DО разделим на n равных частей (точками О₁, О₂, O₃, О₄.)

2. Через эти точки О_i проводим плоскости (сечения) параллельно основанию пирамиды AВС.

3. Через точки пересечения этих сечений с ребрами ВD и СD проводим отрезки параллельно ребру AD, так чтобы они заключались между проведенными соседними параллельными сечениями.

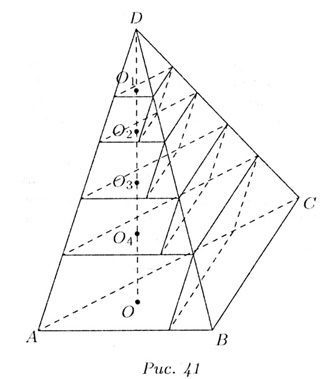
4. Получим «лестницу» уменьшающихся призм, идя от основания ABC к вершине D, но высоты их одинаковые:

Эти призмы отличаются основаниями.

5. Сразу заметим, что если н качестве n брать очень большое число, например n = 10⁶, то объединение всех полученных призм как единое тело мало отличается от первоначальной призмы. Другими словами, объемы этих двух различных тел отличались незначительно друг от друга.

Именно эту идею используем для того, чтобы получить объявленную выше формулу объема пирамиды. Переходим к вычислениям, используя теорему о свойствах параллельных сечений в пирамиде. Если пирамиду пересечь плоскостью, параллельной основанию, то в сечении получается многоугольник, подобный основанию, а площадь сечения и площадь основания относятся как квадраты их расстояний до вершины пирамиды.

Обозначим через S₁,S₂,...S_n-1 площади сечений, проходящих черен точки O₁,O₂,...O_n-1 соответственно, а через V₁,V₂,...V_n-1объемы призм, верхние основания которых содержат точки O₁,O₂,...O_n-1. Имеем

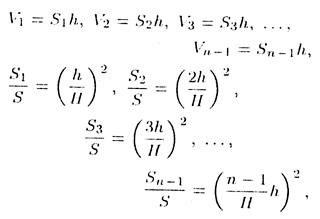
где

Из этих неравенств получаем

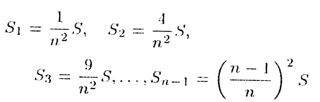
и эти равенства подставлены в формуле для объемов с учетом

Объем «лестницы», составленной из призм, равен

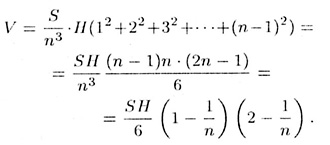
Здесь мы воспользовались известной формулой

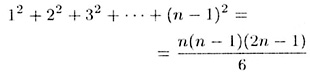
Таким образом, если n — достаточно большое число, то

близко к 0.

а

- близко к 2. Тем самым, получили

а имея в виду, что на самом деле объем пирамиды не зависит от тех построений, которые мы выполняли, то приходим к формуле

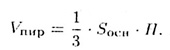
Если необходимо вычислить объем n-угольной пирамиды, то ее можно разбить на n — 2 треугольные пирамиды сечениями, проходящими через вершину пирамиды и диагонали основания, проведенные из общей вершины (основания). Поскольку площадь многоугольника основания равна сумме площадей треугольников, а высоты всех пирамид одинаковы, то доказанная формула остается справедливой и в этом общем случае.