Площадь сферы радиуса R вычисляется по формуле

Около сферы можно описать многогранник с достаточно большим числом граней, объем которого будет достаточно точно выражать объем шара (равного ), а площадь боковой поверхности многогранника — площадь сферы. На рис. 43 показан куб, описанный около сферы. Рассмотрим одну грань описанного многоугольника.

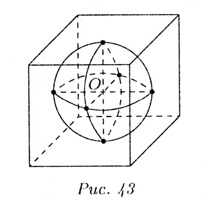
Пирамида, полученная соединением вершин этой грани многогранника с центром сферы, и часть шара, заключенного в этой пирамиде, являются элементами, участвующими в дальнейших рассуждениях и расчетах.

С одной стороны, объем V этой пирамиды высотой R равен

где S_основ — площадь соответствующей грани многогранника. Объем всего многогранника равен сумме объемов таких пирамид с одинаковой высотой R. Сумма их объемов равна

S_бок — площадь боковой поверхности многогранника. С другой стороны, сумма объемов элементов шара равна объему всего шара, равного

Площадь S_бок приближенно равна площади сферы S, а объем многогранника приближенно равен объему шара. Таким образом,

Эти равенства тем точнее, чем большее число граней многогранника. Значит,

Так как в этой формуле но участвуют величины, связанные с многогранником, то формула точна, т. е.