Пусть даны две параллельные плоскости ![]() и
и ![]() , в одной из них некоторая
линия Z и прямая l, пересекающая данные плоскости.
, в одной из них некоторая
линия Z и прямая l, пересекающая данные плоскости.
Если через каждую точку М линии Z провести отрезки MN, параллельные
l и заключенные между ![]() и
и ![]() ,
то множество всех этих отрезков образует поверхность, называемую цилиндрической.
,
то множество всех этих отрезков образует поверхность, называемую цилиндрической.
Движущийся отрезок MN называется образующей поверхности, а линия Z —
направляющей. Если направляющая — окружность, а образующая MN перпендикулярна
плоскостям ![]() и
и ![]() ,
то цилиндрическая поверхность называется прямой круговой (рис. 47, а),
а длина МN — высотой цилиндрической поверхности.
,
то цилиндрическая поверхность называется прямой круговой (рис. 47, а),
а длина МN — высотой цилиндрической поверхности.
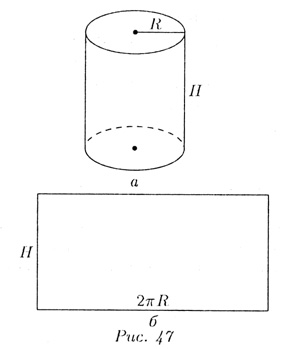
Для определения площади боковой поверхности можно разрезать его по образующей и вытянуть его поверхность в плоскую область. Получаемая поверхность представляет собой прямоугольник с основанием, равным длине окружности основания цилиндра
![]()
(R — радиус окружности) и высотой H (рис. 47,б). Площадь этого прямоугольника равна
![]()
По этой формуле вычисляется площадь боковой прямой цилиндрической поверхности.