Прямая а называется перпендикулярной к плоскости (a _|_ ), если она перпендикулярна любой прямой, лежащей в этой плоскости, проходящей через точку пересечения прямой a и плоскости . Одно из свойств перпендикулярных прямой и плоскости выражается следующим утверждением.

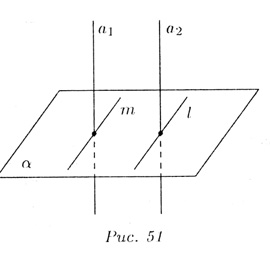
Теорема. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая перпендикулярна этой плоскости.

Пусть а₁|| a₂ и а₁ _|_ .

Надо доказать: а₂ _|_ .

Пусть l — произвольная прямая плоскости , проходящая через точку пересечения прямой a₂ и плоскости (рис. 51). Проведем еще прямую m и плоскости через точку пересечения а₁ с и параллельную l (m || l). Так как а₁ _|_ , то а₁ _|_ m. Кроме этого, соответственно параллельные перпендикулярным прямым сами перпендикулярны. Следовательно, а₂ _|_ l, и так как l — произвольная прямая в , то а₂ _|_ . Теорема доказана.

Сформулируем еще одно свойство перпендикулярности прямой и плоскости.

Теорема. Если две прямые перпендикулярны одной плоскости, то эти прямые параллельны.