В некоторой плоскости 
построим многоугольник (n-угольник)
AI,AZ,—1„,
а вне берем точку Р. Эту точку
соединим отрезками прямых со всеми вершинами многоугольника. Получим n
треугольников
(на рис. 54 изображен случай n = 5).
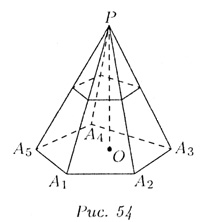
Геометрическая фигура, состоящая из n треугольников и первоначальпого n-угольника, называется пирамидой. Обозначение: PA1A2....An, P — вершина пирамиды. Часть пространства, расположенного внутри пирамиды, также присоединяется к пирамиде. Многоугольник A1A2....An называется основанием, треугольники — боковыми гранями, их стороны — ребрами. Отрезки PA1 , PA2....PAn называются боковыми ребрами, стороны многоугольника — ребрами (сторонами) основания. Отрезок ОР перпендикуляра, опушенного из вершины Р на плоскость основания пирамиды, называется ее высотой.
В виде пирамиды строят купола отдельных зданий.
Треугольная пирамида называется тетраэдром. Плоскость, параллельная основанию пирамиды и пересекающая ее, отсекает подобную пирамиду, а в сечении получается многоугольник, подобный основанию. Оставшаяся часть называется усеченной пирамиды.