В некоторой плоскости ![]() строим правильный многоугольник, n-угольник
строим правильный многоугольник, n-угольник
![]()
Из центра О этого многоугольника (О центр вписанной и описанной окружностей) посставим перпендикуляр, а на нем возьмем некоторую точку Р. Эту точку соединим со всеми вершинами многоугольника (см. рис. 56).
В результате этих построений получим n равных равнобедренных треугольников
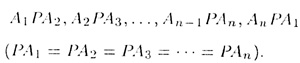
Геометрическая фигура, состоящая из взятого правильного многоугольника и построенных треугольников, называется правильной пирамидой. При n = 3 соответствующая пирамида называется тетраэдром.
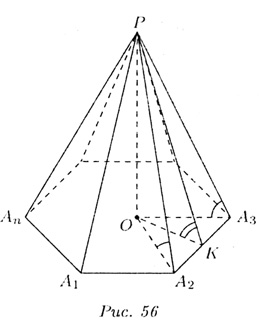
Многоугольник A1A2...An называется основанием, соответствующие треугольники — боковыми гранями, их боковые стороны — боковыми ребрами. Отрезок РО называется высотой пирамиды, а высота РК боковой грани (любой) — апофемой пирамиды. В правильной пирамиде боковые ребра образуют с основанием равные углы, боковые грани — с плоскостью основания образуют также равные углы.