Пространственные фигуры мы изображаем на плоскости (на бумаге, доске и пр.), используя параллельное проектирование. Для этого задаемся некоторой прямой (направлением) l и из каждой точки М пространственной фигуры проводим прямые МN параллельно l до пересечения с плоскостью чертежа (бумаги). Поскольку проектировать все точки фигуры невозможно, мы ограничимся проектированием отрезков (отрезки проектируются в отрезки), для чего достаточно проектировать их копны (рис. 57).
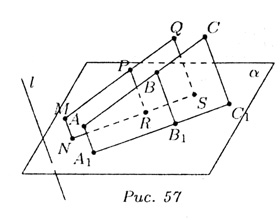
- Прямолинейные отрезки фигуры изображаются на плоскости чертежа отрезками. Прямые MN, PR и QS параллельны, а значит, они лежат в одной плоскости, поэтому MQ проектируется в отрезок NS (пересечение двух плоскостей).
- Параллельные отрезки фигуры изображаются на плоскости чертежа параллельными отрезками.
- Отношение отрезков одной прямой пли параллельных прямых мри параллельном проектировании сохраняется.
Если АB || МР, то их проекции А1В1 и NR также параллельны, так как они являются пересечениями параллельных плоскостей, проходящих через АА1,ВВ1 и MN, PR, соответственно с плоскостью о.
Если А, B и С — три точки па фигуре, а А1, В1, С1 — соответственно их проекции, то
![]()
Эта пропорция вытекает из теоремы Фалеса.