Дана плоскость и некоторая наклонная а к этой плоскости. Пусть а₁ - проекция прямой а на плоскость , причем наклонная а пересекает в точке О (О - основание наклонной), а значит, проекция а₁ также проходит через О. Пусть b — некоторая прямая плоскости , проходящая через О перпендикулярно к а₁ (или а). Тогда b перпендикулярна и прямой a (или а₁). Эти утверждения составляют содержание теоремы о трех перпендикулярах (или обратная к ней теорема).

Теорема. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и самой наклонной. И обратно, если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Дана наклонная МО с проекцией NO и MN _|_ , в частности, MN _|_ NO (рис. 63).

Дано: PQ _|_ NO (т.е. PQ _|_ а₁).

Надо доказать, что PQ _|_ МО (PQ _|_ а).

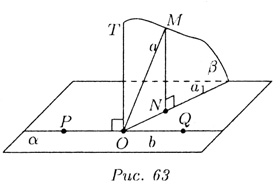
а) Через точку О проводим прямую ОТ, перпендикулярную плоскости . Тогда ОТ || MN, т.к. и MN _|_ и ОТ _|_ . Прямые ОТ и ON образуют плоскость , и PQ перпендикулярна этой плоскости, ибо PQ _|_ ON и PQ _|_ ОТ. Значит, PQ _|_ ОМ, т. е. b _|_ а, т.к. ОM — прямая из плоскости .

Аналогично доказывается и обратная теорема. Если b _|_ а и b _|_ ОТ, то b _|_ (проходящей через ОТ и ОМ), а значит, и проекции а₁, принадлежащей этой плоскости . Теорема доказана.