31.3. В правильной четырехугольной пирамиде высота равна 12 см. а апофема — 15 см. Найти боковое ребро.
Обратимся к чертежу задачи (см. рис. 64).
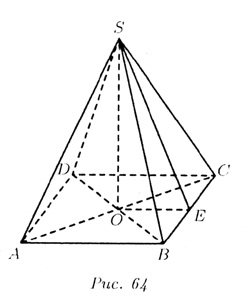
Вершина S правильной четырехугольной пирамиды проектируется в центре О квадрата ABCD. Апофема SE пирамиды перпендикулярна ребру основания ВС. Отрезок ОЕ — проекция апофемы SE на основание, ОЕ _|_ BC. Проекция бокового ребра SC пирамиды на основание совпадет с половиной ОС диагонали АС квадрата ABCD. Треугольники SOE, SOC и ОКС прямоугольные.
1. Из 
SОE по теореме Пифагора
ОE = 9 см.
2. Из ОEС по теореме Пифагора
так как ОЕ = ЕС (диагональ квадрата образует со стороной угол в 45°;
значит, EОС = 45°.
Следовательно,
3. Из SОС по теореме Пифагора
31.4. Ребро куба равно a. Найдите расстояние oт вершины куба до его диагонали, соединяющее две другие вершины.
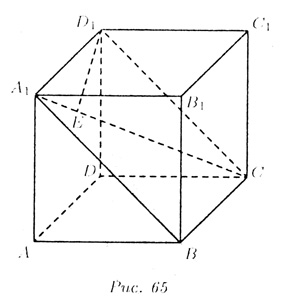
Пусть D1 -- вершина куба, А1С - диагональ куба (рис. 65). Ксли через три псршпиы А1, D1 и С1 куба провести плоскость, то сечением этой плоскостью с поверхностью куба будет прямоугольник А1ВСD1. На диагональ А1С этого прямоугольника опускаем перненднкуляр D1Е из вершины D1. Длина отрезка D1Е и есть искомое расстояние, о котором идет речь в задаче. Егo найдем как высоту прямоугольного треугольника А1D1C (A1D1 _/_ D1,С1, потому что ребро A1D1 куба перпендикулярно грани D1C1CD). Вычисления:
