32.3. Прямоугольный треугольник, гипотенуза которого равна 17 см, а один из катетов — 8 см, вращается около этого катета. Найдите площадь поверхности тела вращения.
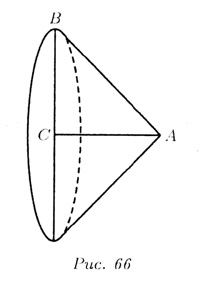
Тело вращения представляет собой конус (рис. 66) с радиусом основания ВС, высотой АС = 8 см и образующей АВ = 17 см.

32.4. Найдите боковую поверхность пирамиды,
если площадь основания равна S, а двугранные углы при основании равны
![]() .
.
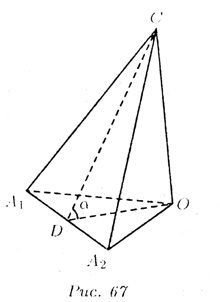
Предположим, что нам задана произвольная n-угольная пирамида СА1 А2 ... Аn, основанием которой является n-угольник А1 А2 ... Аn (С — вершина пирамиды). Боковая поверхность пирамиды равна сумме площадей n треугольников.

а площадь основания равна сумме площадей n треугольников, являющихся проекциями боковых граней (О — проекция вершины С на плоскость основания):
Рассмотрим отношение между площадями
![]()
Пусть CD - высота треугольника СА1A2,
OD — высота треугольника OА1A2.
Тогда OD — проекция CD на основание пирамиды и < СDO =![]() (СDO — линейный угол двугранного угла между боковой гранью СA1А2
и основанием OA1A2).
(СDO — линейный угол двугранного угла между боковой гранью СA1А2
и основанием OA1A2).
Используя формулу площади треугольника, можем записать:

Из прямоугольника CDO имеем OD = CD • cos![]() .
Следовательно.
.
Следовательно.

Авалогичные соотношения будут связывать площадь всех треугольников боковой поверхности и площадь проекций этих треугольников на основание. Поело сложения этих соотношений приходим к равенству