Задача 3
33-3. В правильной треугольной пирамиде боковое ребро равно 4 см. а сторона основания — 6 см. Найдите объем пирамиды.
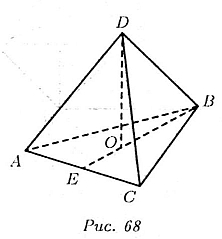
На рис. 68 имеем пирамиду DABC. В ней
AD = BD = CD = 4 см,
АВ = ВС = АС = 6 см.
Объем V вычислим по формуле
![]()
где H = DO — высота пирамиды, О — проекция вершины D на основание, совпадающая
с точкой пересечения медиан, высот, биссектрис, треугольника ABC.
Из треугольника ВЕС со сторонами ВС = 6 см, ЕС = 3 см находим по теореме
Пифагора

Следовательно,
![]()
Из прямоугольного треугольника DOB, по теореме Пифагора,
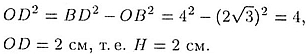
Площадь основания равна
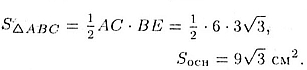
Теперь найдем объем:
![]()
Ответ:![]()
33.4. Два рамных тара радиуса R расположены
так, что центр одного .лежит па поверхности другого. Найдите длину линии,
по которой пересекаются их поверхности.
Сферы, о которых идет роль в ча даче, пересекаются по окружности (см.
рис. 09).

Ее центр О расположен на середине радиуса ![]() данных сфер. Радиус г этой окружности можно найти по теореме Пифагора
из прямоугольного треугольника
данных сфер. Радиус г этой окружности можно найти по теореме Пифагора
из прямоугольного треугольника ![]() ,
где
,
где
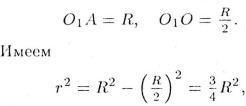
т. е. ![]() . Длина
этой окружности равна
. Длина
этой окружности равна
