1. Квадратное уравнение
ах2 + Ьх + с = О (a # 0)
с дискриминантом
D = b2 - 4ac
имеет:
a) при D >0 — два различных действительных корня:

(вторая формула удобна при четном b); при этом
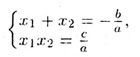
— формулы Виета и
аx2 + bх + с = a(х — x1)(х — x2)
— разложение трехчлена на линейные множители;
b) при D = 0 один корень (говорят также о двух одинаковых или совпадающих корнях х1 — х2 = х0)
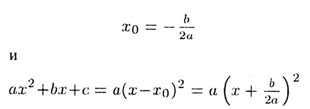
Уравнение
aх2 + bx + с = 0
может иметь один корень, если a = 0 и b # 0;
c) при D < 0 уравнение не имеет действительных корней, а соответствующий квадратный трехчлен на линейные действительные множители не разлагается.
Теорема Виета. Если квадратное уравнение

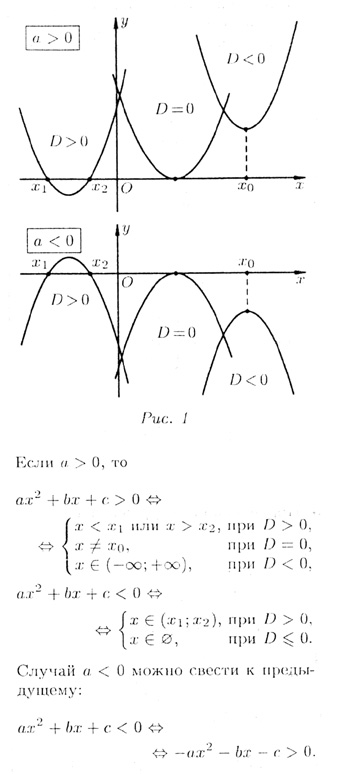
2. На рис. 1 видны промежутки, на которых квадратный трехчлен сохраняет знак.