37.3. В правильной четырехугольной пирамиде сторона основания равна 10 см, а высота — 12 см. Найдите площадь полной поверхности пирамиды.
В основании пирамиды (рис. 76) лежит квадрат ABCD со стороной 10 см. Высота пирамиды EО равна 12 см, О — точка пересечения диагоналей AC и BD квадрата.

Полная поверхность пирамиды равна
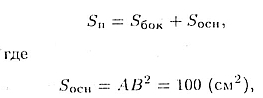
a ![]() боковая
поверхность пирамиды. Грани пирамиды — равные равнобедренные треугольники
и площадь одной грани равна
боковая
поверхность пирамиды. Грани пирамиды — равные равнобедренные треугольники
и площадь одной грани равна
![]()
где ЕК — апофема пирамиды, т.е. высота треугольника BEC. Из треугольника
ОКЕ ![]() со сторонами
со сторонами
![]()
и ОЕ = 12 см находим по теореме Пифагора:
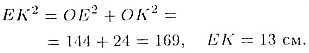
Таким образом,
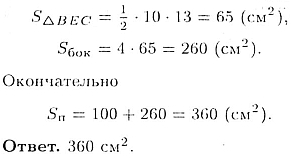
37.4. В цилиндр вписана правильная шестиугольная призма. Найдите угол между диагональю ее боковой грани и осью цилиндра, если радиус основания равен высоте цилиндра.

Ось ![]() цилиндра
и диагональ ВО боковой грани ABCD (рис. 77) призмы являются скрещивающимися
прямыми. Угол между ними равен углу DBC между DB и боковым ребром призмы,
так как
цилиндра
и диагональ ВО боковой грани ABCD (рис. 77) призмы являются скрещивающимися
прямыми. Угол между ними равен углу DBC между DB и боковым ребром призмы,
так как ![]() .
Сторона правильного вписанного шестиугольника равна радиусу цилиндра.
Также радиусу равно ребро BC, т.е. ABCD — квадрат. Угол между стороной
квадрата и его диагональю равен 45°.
.
Сторона правильного вписанного шестиугольника равна радиусу цилиндра.
Также радиусу равно ребро BC, т.е. ABCD — квадрат. Угол между стороной
квадрата и его диагональю равен 45°.
Ответ. 45°.