Задача 9
39.3. В правильной четырехугольной пирамиде высота равная 7 см, а боковое ребро наклонено к плоскости основания под углом 45°. Найдите объем пирамиды.
Основанием пирамиды является квадрат ABCD, ее ребра равны
АЕ = BE = CE = DE
О — проекция вершины Е па основание, и ОЕ — совпадает с точкой пересечения диагоналей, ОЕ = 7 см, угол ОAЕ равен 45° (рис. 80). Объем вычислим по формуле
![]()

1. Треугольник АОE прямоугольный и равнобедренный,
АО = ОЕ = 7 см,
значит, АС = 14 см.
2. Треугольник AВС прямоугольный,
равнобедренный и но теореме Пифагора

Получаем
![]()
3. Вычисляем объем:
![]()
![]()
39.4. Докажите, что площадь поверхности куба равна 2d2, где (d — диагональ куба)
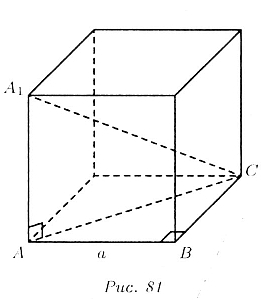
Пусть а — сторона куба (рис. 81). Площадь поверхности равна, площади шести квадратов со стороной а, т.е.
![]()
С другой стороны, из прямоугольных треугольников ABC и AA1C
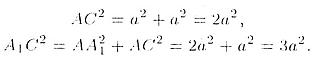
Так как A1С - диагональ куба, то
d2 = За2 .
Выше получили
S = 6a2
значит,
S=2d2
Требуемое доказано.