310.3. Прямоугольник, стороны которого равны 6 см и 4 см, вращается около меньшей стороны. Найдите площадь поверхности тела вращения.

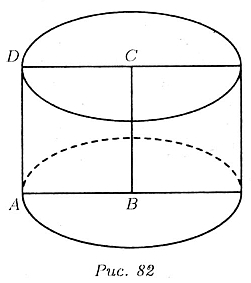
Если прямоугольник ABCD вращать около стороны BC, то получается цилиндрическая поверхность радиуса
R = АB = 6 см
и высотой
H = ВC = 4 см
(рис. 82). Боковая поверхность цилиндра, равна

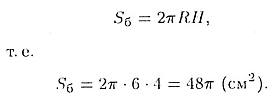
Основания цилиндра с общей площадью это два круга с общей площадью

Вся (полная) поверхность цилиндра имеет площадь, равную

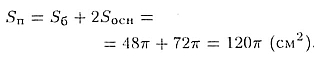
310.4. Докажите, что если данная прямая параллельна двум плоскостям, то она параллельна .пиний их пересечения.
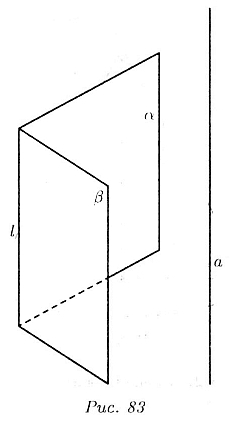
Пусть — две плоскости, которые пересекаются по прямой l (рис. 83). Пусть а — прямая, параллельная , т.е. a не имеет общих точек ни с плоскостями .
Пало доказать, что а || l.
Мы будем пользоваться свойством транзитивности: если две прямые параллельны третьей прямой, то они параллельны между собой.

Если , то а параллельна некоторой прямой . Аналогично
a || b₁ , где . По свойству транзитивности a₁ || b₁.Так как То отсюда следует, что
Докажем, что a₁ || l. Если бы a₁пересекала прямую l, то она пересскапа бы плоскость , ибо , но это невозможно, так как
Итак, a₁ не пересекает l, и так как эти дне прямые лежат и одной плоскости , то они параллельны.
Мы получили, что a₁ || l , и a || a₁, следовательно, по свойству транзитивности, а || l