311.3 Основание четырехугольной призмы — квадрат со стороной 10 см, высота призмы 12 см. Диагональное сечение разбивает данную призму на две треугольные призмы. Найдите площади боковых поверхностей треугольных призм.

Дана, призма ABCDA₁B₁C₁D₁. Ее основания ранные квадраты ABCD и A₁B₁C₁D₁

А В = 10 см,

высота H — 12 см (рис. 84). Диагональное сечение АА₁С₁С делит призму на две, равные треугольные призмы. Основание каждой — равнобедренный треугольник, высота — H. Площадь боковой поверхности призмы ABCA₁B₁C₁ равна

Найдем АС из треугольника ABC по теореме Пифагора

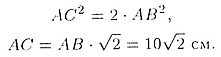
Таким образом,

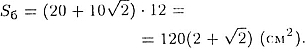
311.4. В правильной треугольной пирамиде высота равна стороне основания. Найдите yгол между боковым ребром и плоскостью основания.

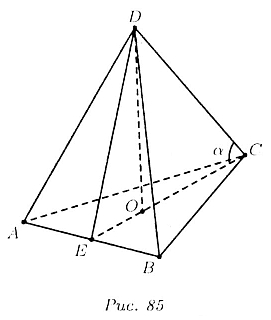
В пирамиде ABCD известно, что

AD =BD = CD

AB= BC= AC= DO

где О — проекция вершины D на основание AВС. Пусть

B = а и

(рис. 85). Из Треугольника EBC находим

Точка О лежит на пересечении медиан, поэтому

Из треугольника DOC по определению тангенса можем записать

Отсюда следует, что = 60°
Ответ. 60°.