316.3. Осевым сечением цилиндр
является, квадрат, диагональ которого равна ![]() см.
Найдите площадь поверхности цилиндра.
см.
Найдите площадь поверхности цилиндра.
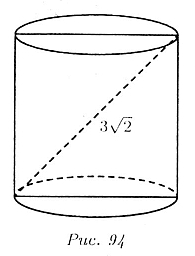
Сторона квадратного сечения является высотой цилиндра, и диаметром его
основании (рис. 94). Если сторона квадрата равна а, то его диагональ равна
![]() . Следовательно,
если диагональ равна
. Следовательно,
если диагональ равна ![]() см. то сторона равна 3 см, значит, высота H цилиндра равна 3 см, а радиус
основания R ранен 1,5см. Площадь поверхности (полной) цилиндра равна
см. то сторона равна 3 см, значит, высота H цилиндра равна 3 см, а радиус
основания R ранен 1,5см. Площадь поверхности (полной) цилиндра равна

![]()
316.4. Плоскость параллельная основанию конуса, делит его боковую поверхность на две части, площади которых равны. В каком отношении, считая от вершины, эта плоскость делит высоту конуса?
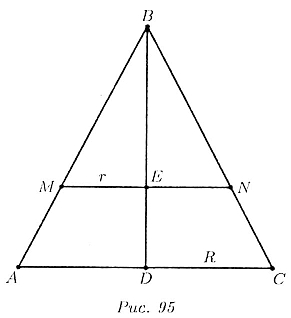
На рис. 95 изображено осевое сечение конуса (треугольник ABC), MN — сечение
конуса плоскостью, параллельной основанию AС, прямая BD — ось конуса,
точка E — пересечение оси с отрезком MN. Площадь боковой поверхности конуса
MBN равна ![]() ,
где
,
где
r = ME = EN, l = MB = BN
а площадь конуса AВС равна
![]()
![]()
где
R = DC, L = BС.
Из условия задачи
![]()
Прямоугольные треугольники ABD и MBE подобны, и пусть k — их коэффициент подобия:
![]()
С другой стороны,
![]()
Значит,
![]()
Из равенства ![]() получаем, что
получаем, что
![]()
Последнее равенство означает, что плоскость MN делит высоту конуса BD на отрезки BE и ED в отношении
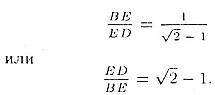
В условии задачи требуется отношение ![]() .
Оно равно
.
Оно равно
