318.3. В прямоугольном параллелепипеде стороны основания равны 5 см и 12 см, а диагональ параллелепипеда наклонена к плоскости основания под углом 45°. Найдите высоту параллелепипеда.
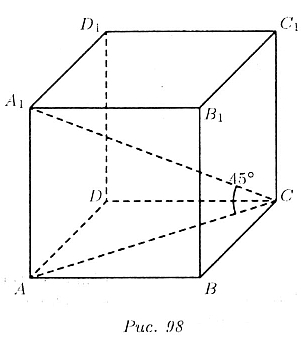
В прямоугольном параллелепипеде ABCDA1B1C1D1
(рис. 98) боковое ребро AA1 перпендикулярно плоскости основания
ABCD, а значит оно перпендикулярно любой прямой из этой плоскости, в частности
АС. Поэтому ![]() —
прямоугольный угол A1AC = 90°. При этом А1С — диагональ
параллелепипеда, АС — ее проекция на плоскость основания и по условию
задачи угол A1CA= 45°. Cледовательно
—
прямоугольный угол A1AC = 90°. При этом А1С — диагональ
параллелепипеда, АС — ее проекция на плоскость основания и по условию
задачи угол A1CA= 45°. Cледовательно ![]() — прямоугольный равнобедренный (угол AA1C= 45°) поэтому AA1
= AC, т.е. высота параллелепипеда. которую надо oпределить, равна диагонали
основания.
— прямоугольный равнобедренный (угол AA1C= 45°) поэтому AA1
= AC, т.е. высота параллелепипеда. которую надо oпределить, равна диагонали
основания.
Так как ABCD — прямоугольник то треугольник ABC прямоугольный с катетам
AB = 12 см, BС = 5 см, а тогда по теореме Пифагора,
![]()
Ответ. 13 см
318.4. Площадь боковой поверхности цилиндра равна Q. Найдите площадь осевого сечения.

Площадь боковой поверхности цилиндра равна
![]()
где; R — радиус, H — высота цилиндра (рис. 99). Осевое сечение цилиндра — прямоугольник, одна сторона которого — высота цилиндра, а другая — диаметр основания. Таким образом, площадь осевого сечения равна
![]()
![]()