319.3. В правильной четырехугольной пирамиде сторона основания равна 12 см, а апофема — 15 см. Найдите боковое ребро пирамиды.
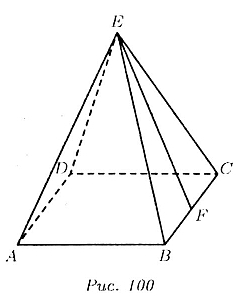
Основанием правильной пирамиды является квадрат AВСD со стороной B =
12 см. Боковые грани пирамиды — равные равнобедренные треугольники (рис.
100).
Апофемой пирамиды является высота ЕF боковой грани ВЕС. Следовательно,
треугольник ЕFС прямоугольный, и в нем ЕF = 15 см, a FC = 6 см. По теореме
Пифагора
EС2 = ЕF2 + FC2,
т. е.
ЕС2 = 152 + 62 =261
Значит,
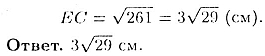
319.4. Дан прямоугольный пapaллелепипед.
Угол между диагональю основания и одной из его сторон равен ![]() .
Угол между этой стороной и диагональю параллелепипеда равен
.
Угол между этой стороной и диагональю параллелепипеда равен ![]() .
Найдите площадь боковой поверхности параллелепипеда, если диагональ основания
равна k.
.
Найдите площадь боковой поверхности параллелепипеда, если диагональ основания
равна k.

Все грани параллелепипеда AВСDA1В1С1D1
являются прямоугольиками (рис. 101).
По условию
![]()
Боковая поверхность параллелепипеда состоит из двух пар равных прямоугольников:
![]()
1. Из ![]() находим
находим
![]() ,
, ![]()
2. Из ![]() (поскольку
АB перперндикулярно грани AA1D1D , то AB перпендикулярно
любой прямой из этой рани, а значит,
(поскольку
АB перперндикулярно грани AA1D1D , то AB перпендикулярно
любой прямой из этой рани, а значит, ![]() )
находим
)
находим ![]()
3. Из треугольника ADD1 по теореме Пифагора
(DD1)2 = (AD1)2 - (AD)2
Следовательно,
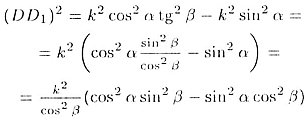
Используя формулу синуса суммы и разности двух углов получаем
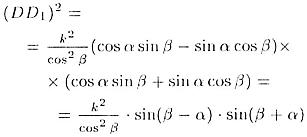
Наконец,
![]()
Теперь можно вычислить требуемую площадь

