которая позволяла бы приписать неизвестному параметру рассматриваемого объекта некоторое числовое значение (оценку) , причем эта оценка зависит от последовательности наблюдений , где - есть управление. Рассматриваемая ситуация изображена на рис.1.

Часто подразумевается, что идентификация начинается из ”ничего” без всякой априорной информации об объекте. Но в большинстве технических задач такое предположение не реалистично; из структуры объекта и, по крайней мере, частичного понимания его функционирования можно извлечь определенную априорную информацию и, в частности, вид структуры модели. В этом случае остается только получить информацию о числовых значениях ряда параметров (коэффициентов дифференциальных уравнений, описывающих динамику объекта, и т. д.). В результате задача идентификации сводится к задаче оценивания параметров. Под оцениванием параметров понимается экспериментальное определение значений параметров, характеризующих динамику поведения объекта, в предположении, что структура модели объекта известна.

При оценивании используют различные виды оценок, которые различаются объемом исходной информации об объекте. Например, при нахождении оценки по методу наименьших квадратов предполагается, что динамика объекта может быть аппроксимирована выбранной моделью. При получении ”марковских” оценок считается также известной ковариационная матрица шума. Для вычисления оценок максимального правдоподобия необходимо знание плотности вероятности измеряемого случайного процесса. Байесовские оценки, или оценки с минимальным риском, требуют знания априорных плотностей вероятности неизвестных параметров и величины штрафа за ошибки.

В данной работе мы будем рассматривать частный случай показанной выше ситуации, т.е. рассмотрим параметрическое оценивание параметров динамической системы без управления, а неизвестные параметры будем оценивать методом максимального правдоподобия.

Известно, что при оценивании существенный интерес представляет информация о рассматриваемых параметрах, в частности плотность вероятности или . Эта функция зависит от продолжительности интервала наблюдений или, что то же самое, от размера выборки и представляет собой наиболее полную информацию, которую можно получить, применяя статистические методы.

Пусть известна плотность вероятности шума . По ней можно рассчитать плотность вероятности измерений , которая зависит от параметров объекта и обозначается через . Также положим, что априорное распределение вероятностей параметра в области возможных значений параметра. Тогда разумно выбирать , совпадающее со значением , максимизирующим . В соответствии с формулой Байеса

для произвольного имеем

Априорная плотность вероятности имеет вид

Апостериори после измерений выборочных значений , или , совместная плотность вероятности обозначается как

и называется функцией правдоподобия. По функции правдоподобия находиться оценка , причем логично выбирать такое значение , которое максимизирует . Тогда необходимое условие максимума имеет вид

или в силу монотонности логарифма

Эту формулу называют уравнением правдоподобия и, отыскивая решение этой системы уравнений, которое обеспечивает наибольшее значение или , находим оценку максимального правдоподобия , а, находя оценку максимального правдоподобия, мы тем самым находим неизвестные параметры системы.

Таким образом, задача оценивания может быть сформулирована как задача нахождения наибольшего (наименьшего) значения некоторого функционала. Но т.к. значения параметров непосредственному наблюдению не доступны, то критерием выбора оптимума должен быть функционал от выходных сигналов или от математического ожидания ошибок оценок параметров. Примером такого функционала может служить либо функция правдоподобия, либо ее логарифм. Т.е. если - это выход объекта, -соответствующий выход модели и, также когда, невязки ошибок предсказания являются независимыми и имеют гауссовское совместное распределение с нулевым средним и матрицами ковариаций , тогда выражение для обратного логарифма функции максимального правдоподобия имеет следующий вид:

Тогда нахождение оценки максимального правдоподобия эквивалентно минимизации следующего функционала:

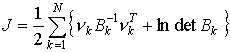(1.2.1)

Тогда

Критерием выбора оптимума, в нашем случае этим критерием есть выражение (1.2.1), является функция (функционал) многих переменных и для ее минимизации будем использовать наиболее известные и часто применяемые методы минимизации функций многих переменных.

В общем случае будем рассматривать задачу

(1.3.1)

предполагая, что функция непрерывно дифференцируема на . Согласно определению дифференцируемости функции

(1.3.2)

где . Если , то при достаточно малых главная часть приращения (1.3.2) будет определяться дифференциалом функции . Справедливо неравенство Коши-Буняковского

причем если , то правое неравенство превращается в равенство только при , а левое неравенство – только при , где . Отсюда ясно, что при направление наибыстрейшего возрастания функции в точке совпадает с направлением градиента , а направление наибыстрейшего убывания – с направлением антиградиента .

Это замечательное свойство градиента лежит в основе ряда итерационных методов минимизации функций. Одним из таких методов является градиентный метод, к описанию которого мы переходим.

1. Градиентный метод. Будем считать, что некоторая точка уже выбрана. Тогда метод заключается в построении последовательности по правилу:



Существуют различные способы выбора в данном методе, но на практике нередко довольствуются нахождением какого-либо , обеспечивающего условие монотонности: . С этой целью задаются какой-либо постоянной и на каждой итерации метода берут . При этом для каждого проверяют условие монотонности, и в случае его нарушения дробят до тех пор, пока не восстановится монотонность метода.

2. Метод Ньютона. Градиентный метод является методом первого порядка, поскольку использует лишь первые производные минимизируемой функции. Однако если минимизируемая функция дважды непрерывно дифференцируема и производные вычисляются достаточно просто, то возможно применение метода минимизации второго порядка, которые используют квадратичную часть разложения этой функции в ряд Тейлора. Широко известный метод Ньютона представляет собой итерационный процесс:



3. Метод сопряженных направлений. Метод сопряженных направлений является методом использующим лишь градиент функционала и описывается следующим образом:

где величина находится из условия

а вычисляется из следующих формул

Точное определение величины возможно лишь в редких случаях, поэтому реализация каждой итерации метода будет сопровождаться неизбежными погрешностями. Эти погрешности, накапливаясь, могут привести к тому, что векторы перестают указывать направление убывания функции, и сходимость метода может нарушиться. Чтобы бороться с этим явлением, метод сопряженных направлений время от времени обновляют, полагая .

Пусть динамическая система с дискретным временем дана в следующем виде:

(1.4.1)

где вектор состояния , матрица переходов из состояния в состояние , и - случайный процесс, представляющий собой белый гауссовый шум с нулевым средним и ковариацией , т.е. .

Пусть множество наблюдений задается уравнением:

(1.4.2)

где вектор наблюдения , матрица наблюдений , и - шум: .

Предположим, что мы имеем априорный информационный массив , где - невырожденная априорная ковариация и оценки относятся к и следующим образом:

; (1.4.3)

где есть экстраполяционная оценка вектора состояния, а - матрица ковариации ошибки экстраполяционной оценки.

Замечание: Для отфильтрованной оценки и ее матрицы ковариаций связь с информационным массивом аналогична.

Предполагая, что мы можем записать следующее равенство:

(1.4.4)

Тогда модель наблюдений и предсказания выглядит следующим образом:

(1.4.5)

(1.4.6)

где , , - ортогональные матрицы такие, что матрицы и являются верхнетреугольными, а - остаточная ошибка, соответствующая решению наименьших квадратов.

Заметим, что уравнения (1.4.5) и (1.4.6) эквивалентны уравнениям фильтра Калмана (доказательство данного факта см. в [2]). Но в отличие от традиционного фильтра Калмана, ККИФ позволяет избежать численной неустойчивости, являющейся результатом вычислительных погрешностей, поскольку вместо матриц ковариаций ошибки оценок на этапах экстраполяции и обработки измерений, по своей природе положительно определенных, ККИФ оперирует с их квадратными корнями. А это значит, что вычисления квадратного корня равносильно счету с двойной точностью для ковариации ошибок и кроме того устраняется опасность утраты матрицей ковариаций свойства положительно определенности. Недостатком данного метода является присутствие операций извлечения квадратного корня.

Вычисление оценки максимального правдоподобия может быть итеративно выполнено при помощи характеристического уравнения, которое включает в себя градиент обратного логарифма функции правдоподобия и информационную матрицу Фишера. Вычисления функции правдоподобия и информационной матрицы Фишера требуют применения фильтра Калмана (а также его производных для каждого параметра оценивания), который, как известно, не обладает достаточной устойчивостью. Поэтому для вычисления оценки максимального правдоподобия итеративным образом будем использовать ККИФ.

Пусть динамическая система с дискретным временем дана в следующем виде:

(2.1.1)

где вектор состояния , матрица переходов из состояния в состояние , и - случайный процесс, представляющий собой белый гауссовый шум с нулевым средним и ковариацией , т.е. . Пусть множество наблюдений задается уравнением:

(2.1.2)

где вектор наблюдения , матрица наблюдений , и - шум: .

Пусть также, матрицы и являются функциями неизвестного векторного параметра .

Оценкой максимального правдоподобия является такое значение оцениваемых параметров , которое максимизирует вероятность события, при котором наблюдения, сгенерированные с подстановкой оцениваемых параметров, совпадают с действительными значениями наблюдений . Эта процедура эквивалентна минимизации обратного логарифма функции плотности условной вероятности, т.е. обратный логарифм функции правдоподобия представляется как:

(2.1.3)

где и - вычисляются согласно схеме фильтра Калмана следующим образом:

(2.1.4)

где есть ковариационная матрица ошибки экстраполяционной оценки.

Запишем другие характеристики фильтра Калмана, которые нам понадобятся в дальнейшем:

Матрица Калмана:

(2.1.5)

Матрица ковариаций измененной по последним данным ошибки:

(2.1.6)

Невязка:

(2.1.7)

Измененная оценка:

(2.1.8)

Вычисление оценки максимального правдоподобия может быть осуществлено итеративно по следующей формуле:

(2.1.9)

где - оцениваемый векторный параметр; - индекс, определяющий номер итерации; - информационная матрица Фишера; - градиент обратного логарифма функции максимального правдоподобия.

Стоит заметить, что итеративные алгоритмы, подобные (2.1.9), в среднем сходятся за меньшее число шагов, чем те алгоритмы, которые включают в себя только вычисления . С другой стороны, алгоритмы, содержащие и , требуют больше вычислений на каждом шаге.

Модель наблюдений, в случае ККИФ, выглядит следующим образом:

(2.1.10)

где - ортогональная матрица такая, что - верхнетреугольная. Также, согласно (2.1.2) имеют вид:

(2.1.11)

где

(2.1.12)

тогда шум наблюдения имеет единичную ковариацию, что удовлетворяет ККИФ.

Шаг предсказывания ККИФ, описывается следующим образом:

(2.1.13)

где матрица представляется уравнением (1.4.4), - ортогональная матрица такая, что матрица является верхнетреугольной.

Информационным массивом ККИФ является массив данных . Он соотносится с оценкой состояния фильтра Калмана и матрицей ковариации ошибки оценивания следующими соотношениями:

(2.1.14)

(2.1.15)

Для эффективного вычисления функции максимального правдоподобия при использовании ККИФ в фильтрации данных, необходимо выразить величины, входящие в выражение для , непосредственно через значения, которые вычисляются ККИФ-ом. Таким образом, две части (2.1.3):

(часть, зависящая от данных) (2.2.1)

(часть, зависящая от модели) (2.2.2)

выраженные через переменные, входящие в формулы ККИФ (2.1.10) и (2.1.13), приобретают следующий вид:

(2.2.3)

(2.2.4)

Доказательство (2.2.3) основано на следующем уравнении:

где - ортогональное преобразование такое, что матрица - верхнетреугольная. Находя нормы от обеих частей равенства, получим:

Уравнение (2.1.14) влечет за собой, следующее выражение:

Следовательно:

Далее, используя (2.1.8), чтобы переписать данное выражение в следующем виде:

После раскрытия скобок, опять используя уравнение (2.1.14), имеем:

Далее следует:

(2.2.5)

Наконец, используя (2.1.4), (2.1.5) и (2.1.15), получаем, что матрица, находящаяся внутри квадратных скобках выражения (2.2.5), является просто матрицей , что и доказывает (2.2.3).

Доказательство (2.2.4) основано на существовании ортогональных преобразований между определенными переменными ККИФ и остаточной ковариационной матрицей. Для упрощения записи положим, что

Используя обычную матричную алгебру и уравнения (2.1.4), (2.1.5), (2.1.6) и (2.1.15) можно показать, что выполняется следующее равенство:

Следовательно, если положить

(2.2.6)

получаем, что

- ортогональная матрица. Переписав (2.2.6) в виде

имеем

Из выражений для и получаем значения для детерминантов:

тогда имеем

Взяв логарифм от обеих частей выше записанного выражения и используя тот факт, что

получаем верное тождество для (2.2.4).

Простое преобразование формул, полученных выше, где шум наблюдения или измерения также является зависимым параметром, дает следующую формулу обратного логарифма функции правдоподобия в терминах ККИФ:

Для вычисления градиента , прежде всего, заметим, что градиент части, зависящей от модели (см. (2.2.2)), записывается следующим образом:

Так как матрицы и треугольные, а точнее верхнетреугольные, то только их диагональные элементы должны быть вычислены. Диагональные элементы первых трех матриц могут быть вычислены недорогим частичным обращением соответствующих величин ККИФ. Диагональные элементы последних двух матриц могут быть вычислены с использованием метода, описанного в разделе 2.4.

Для градиента части, зависящей от данных, функции максимального правдоподобия, мы используем соотношение для изменения уравнений измерения ККИФ:

где - ортогональная матрица. Находя нормы от обеих частей равенства, получаем что:

Из последнего равенства имеем, что:

где значения может быть получено дифференцированием ККИФ, как показано в разделе 2.4. Значения матрицы получаются путем дифференцирования соотношения:

Таким образом:

(2.3.1)

Между тем, матрица - верхнетреугольная и должна равняться , где - верхнетреугольная часть матрицы на левой стороне (2.3.1) и - диагональная часть. И тогда, находится с помощью метода обратной подстановки решения треугольных систем.

Подводя итог выше сказанному, имеем, что градиент обратного логарифма функции максимального правдоподобия приобретает вид:

,

где все входящие величины являются либо входными значениями КИИФ, либо легко находятся путем решения треугольных систем.

Для выражения информационной матрицы Фишера в терминах ККИФ, вспомним, что - ый элемент матрицы Фишера записывается как:

Т.к. - случайный процесс с нулевым средним, то

(2.3.2)

где - -ая величина во временной последовательности, представляющей . Переписывая (2.3.2), используя ККИФ-форму представления , имеем, что - ый элемент матрицы Фишера приобретает вид:

Эта формула может быть использована и при замене ожидаемых значений переменных и вычисленными.

Теперь дадим численно эффективный и точный метод для вычисления значений, , которые необходимы в формулах раздела 2.3.

Для упрощения понимания положим, что преобразования ККИФ (2.1.10) и (2.1.13) имеют вид:

(2.4.1)

где - прямоугольная матрица, - ортогональная, которая при умножении с дает верхнюю трапециевидную матрицу . Элементы матрицы дифференцируемые функции параметра . Тогда, при заданных значениях производных , мы хотим определить матрицу . Явно прослеживается обобщение на случай ККИФ - преобразований и параметр заменяется вектором . Вдобавок, мы потребуем, чтобы и, следовательно, были квадратными и невырожденными.

Для более полного представления ситуации, вначале остановимся на достаточно очевидном решении этой проблемы, однако, которое может вызвать определенные вычислительные трудности и, поэтому, не рекомендуется. Данный подход основан на использовании (2.4.1) и решении следующего уравнения:

далее прямое дифференцирование дает:

(2.4.2)

Используя тот факт, что и, следовательно, - верхнетреугольные, (2.4.2) может быть использовано для вычисления элементов . Для этого применяется алгоритм прямой подстановки, который является стандартным алгоритмом решения линейных систем. Вычислительные сложности могут возникнуть, когда матрица и, следовательно, плохо обусловлены (т.е. почти вырождены). Алгоритм прямой подстановки в этом случае может давать, мягко говоря, неточные результаты.

Выбранный метод базируется на том наблюдении, что если матрица - ортогональная, то выполняется следующее равенство: . Дифференцируя это уравнение, находим, что

или (2.4.3)

Матрица , которая удовлетворяет соотношению - кососимметричная. Очевидно, что такая матрица имеет следующий вид: , где - строго нижнетреугольная. Поэтому (2.4.3) можно переписать в следующем виде:

(2.4.4)

для некоторой нижнетреугольной матрицы .

Лемма: Нижнетреугольная матрица в соотношении (2.26), где удовлетворяет

(2.4.5),

Продифференцировав равенство (2.4.1), получаем:

(2.4.6)

из которого имеем:

Используя тот факт, что

получаем, что

(2.4.7)

Далее, так как и верхнетреугольные матрицы, то и и также верхнетреугольные. Поэтому, нижнетреугольная часть должна в точности соответствовать нижнетреугольной части с обратным знаком. Следовательно, если , то

Уравнение (2.4.7) дает метод для вычисления . Подстановкой (2.4.5) и (2.4.4) в (2.4.7) получаем, что

(2.4.8)

и, таким образом, имеем

Тем самым получаем путь нахождения :

• вычислить ;
• привести к виду ;
• вычислить

и результатом будет .

Уравнение (2.4.8) показывает всю опасность применения (2.4.6) непосредственно. Из соотношения (2.4.8) находим:

Первым слагаемым является , а вторым - . Записанное в таком виде соотношение (2.4.8), включает и в первое, и во второе слагаемое матрицу , но с разными знаками. Более того, матрица полная, то есть исключение происходит по всей матрице . Если значение матрицы небольшие, в сравнении с элементами матриц и , тогда сумма вычисляется достаточно точно. Однако если некоторые из элементов велики, тогда соответствующие элементы суммы будут неточны вследствие большого исключения элементов и результат в целом будет неточен.

Идеи, высказанные в разделе 2.4, могут быть использованы для создания очень небольшого и сжатого алгоритма вычисления обратного логарифма функции правдоподобия, его градиента и величин, входящих в выражение для информационной матрицы Фишера.

Пусть определяет собой вектор параметров, по которым функция правдоподобия должна быть продифференцирована. Для вычисления , для каждого i, мы преобразуем уравнение изменения параметров наблюдающей модели следующим образом:

М1: Заменим (2.1.10) на

,

где первые два столбца повторяются для каждого .

М2: Вычислить для каждого :

М3: Вычислить для каждого :

Заметим, что на шаге М2, матрица, которая должна быть обращена верхнетреугольная. Следовательно, результат обращения может быть получен с помощью метода обратной подстановки.

Метод раздела 2.4, для нахождения величин , мы не можем применить напрямую к уравнению предсказания состояния (2.1.13), т.к. матрица, которая должна быть приведена к треугольному виду неквадратная, следовательно, необратимая. Однако этот алгоритм может быть применен при работе с подматрицами.

Т1: Заменим (2.1.13) следующим соотношением:

где первые два столбца повторяются для каждого и , как в (2.1.13)

Т2: Вычислить для каждого :

здесь * - обозначение для первых q столбцов, не представляющих для нас интереса.

Т3: Вычислить для каждого :

Соотношение для определяется дифференцированием уравнения:

и заменой производной , используя (2.4.4), значением вычисленным на шаге Т1. Заметим также, что , необходимое для этого последнего уравнения, легко вычисляется, т.к.

где - верхнетреугольная.

Но самое интересное, что значения , необходимые для вычисления матрицы Фишера, вычисляются автоматически на шаге М3.

Тема работы ”Адаптивное параметрическое оценивание квадратно-корневым информационным алгоритмом” продиктована необходимостью проведения широкого спектра исследований по сравнительным оценкам различных подходов к проблеме идентификации моделей систем.

Новизна и привлекательность рассматриваемого подхода обусловлены соединением в нем известного критерия максимума правдоподобия с алгоритмом квадратно-коневого информационного фильтра. Последний отличается высокой численной устойчивостью к погрешностям вычислений и к случаям плохой обусловленности схемы наблюдений. Однако факт совпадения оценок максимального правдоподобия с параметрами оптимального фильтра в общем случае не доказан. Этим объясняется актуальность экспериментальных исследований, устанавливающих условия, в которых данный критерий и соответствующий алгоритм идентификации могут считаться практически пригодными. М.Кудрявцев проанализировал заданный алгоритм, отличающийся сложным и разнообразным математическим аппаратом, сочетающим методы математической статистики, оптимального оценивания и матричных вычислений. Он обосновал вычислительные компактные схемы, включая вычисление обратного логарифма функции правдоподобия, его градиента по параметру неопределенности и информационной матрицы Фишера, и разработал необходимые программы.

Основательность и настойчивость позволили М.Кудрявцеву выполнить эту работу без лишней торопливости, с глубоким пониманием существа вопроса и доведением всего исследования до наглядных экспериментальных результатов. Работа демонстрирует высокую подготовку ее автора по специальности ”Прикладная математика”, его способности к проведению самостоятельных исследований и заслуживает отличной оценки.

Д.т.н., профессор И.В. Семушин

Спектральный анализ - это один из методов обработки сигналов, который позволяет охарактеризовать частотный состав измеряемого сигнала. Преобразование Фурье является математической основой, которая связывает временной или пространственный сигнал (или же некоторую модель этого сигнала) с его представлением в частотной области.

К обработке сигналов в реальном масштабе времени относятся задачи анализа аудио, речевых, мультимедийных сигналов, в которых помимо трудностей, связанных непосредственно с анализом спектрального содержания и дальнейшей классификацией последовательности отсчетов (как в задаче распознавания речи) или изменения формы спектра - фильтрации в частотной области (в основном относится к мультимедийным сигналам), возникает проблема управления потоком данных в современных вычислительных системах. Реальность накладывает отпечаток как на сами вычислительные алгоритмы, так и на результаты экспериментов, поднимая вопросы, с которыми не сталкиваешься при обработке всей доступной информации.

При обработке сигналов обычно приходится решать задачи двух типов - задачу обнаружения и задачу оценивания. При обнаружении нужно дать ответ на вопрос, наблюдаем ли в данное время некоторый сигнал с априорно известными параметрами. Оценивание - это задача измерения значений параметров, описывающих сигнал [1].

Сигнал часто зашумлен, на него могут накладываться мешающие сигналы. Поэтому для упрощения указанных задач сигнал обычно разлагают по базисным составляющим пространства сигналов. Для многих приложений наибольший интерес представляют периодические сигналы. Вполне естественно, что используются Sin и Cos . Такое разложение можно выполнить с помощью классического преобразования Фурье.

При обработке сигналов конечной длительности возникают интересные и взаимозависимые вопросы, которые необходимо учитывать в ходе гармонического анализа. Конечность интервала наблюдения влияет на обнаружимость тонов в присутствии сильных шумов, на разрешимость тонов меняющейся частоты и на точность оценок параметров всех вышеупомянутых сигналов.

На настоящее время существует большое количество алгоритмов и групп алгоритмов, которые так или иначе решают основную задачу спектрального анализа: оценивание спектральной плотности мощности, с тем чтобы по полученному результату судить о характере обрабатываемого сигнала .Основной вклад сделан такими исследователями как : Голд Б. (Gold B.), Рабинер Л. (Rabiner L.R.) , Бартлетт M. (Bartlett M.S.) Однако каждый из алгоритмов имеет свою область приложения. Например, градиентные адаптивные авторегрессионные методы не могут быть применены к обработке данных с быстро меняющимся во времени спектром. Классические методы имеют широкую область применения, но проигрывают авторегрессионным и методах, основанных на собственных значениях, по качеству оценивания. Но в реальном масштабе времени использование последних затруднено из-за вычислительной сложности.

Более того, применение каждого из методов обычно требует выбора значений параметров (выбор окна данных и корреляционного окна в классических методах, порядка модели в авторегрессионном алгоритме и алгоритме линейного предсказания, предполагаемого числа собственных векторов в пространстве шума в метода Писаренко) и правильный выбор требует экспериментальных результатов с каждым классом алгоритмов.

Таким образом, имеется следующая задача :

Из вышесказанного можно сформулировать следующие подзадачи:

II . анализ классических алгоритмов блочной обработки всей последовательности в части применения окон данных и корреляционных окон

1. анализ алгоритмов обработки сигналов в реальном масштабе времени